Valoración de los modelos lineales. Observaciones atípicas e influyentes
Una forma razonada de determinar si una observación es influyente en un modelo estudiado es estimar la ecuación de regresión con esta observación y sin ella. Si los parámetros obtenidos no varían mucho, se podría concluir que la observación no es influyente. Sin embargo, si los parámetros calculados cambian al no considerar dicha observación se podría concluir que dicha observación si es influyente. Vamos a valorar la influencia de cada una de las observaciones en el modelo mediante diferentes indicadores y medidas de influencia (Cook and Weisberg 1982; Altman and Krzywinski 2016a; Altman and Krzywinski 2016b). En la FIGURA 1 se muestra gráficamente el efecto de estas medidas sobre una observación (Weiner et al. 2003; Fox 1997).
par(mfrow = c(1,3), mar = c(0.5,1,1,0.5))
plot(x = -5, y = -5, xlim = c(0,5), ylim = c(0,5),
axes = TRUE, tcl = NA, yaxt = "n", xaxt = "n",
xlab = "", ylab = "")
abline(h = 0:5, lty = 3, col = gray(0.7))
abline(v = 0:5, lty = 3, col = gray(0.7))
x <- seq(1,2.5, length = 5)
y <- 0.5 + x + rnorm(5, mean = 0, sd = 0.1)
points(x, y, pch = 16, cex = 1.2)
x1 <- 1.75
y1 <- 0.50
points(x = x1, y = y1, pch = 8, cex = 1.2)
abline(lm(y~x), lty = 2, lwd = 1)
x1 <- c(x,x1)
y1 <- c(y,y1)
abline(lm(y1~x1), lwd = 1)
text(x = 0.2, y = 4.8, labels = "a)", cex = 1.2)
plot(x = -5, y = -5, xlim = c(0,5), ylim = c(0,5),
axes = TRUE, tcl = NA, yaxt = "n", xaxt = "n",
xlab = "", ylab = "")
abline(h = 0:5, lty = 3, col = gray(0.7))
abline(v = 0:5, lty = 3, col = gray(0.7))
x <- seq(1,2.5, length = 5)
y <- 0.5 + x + rnorm(5, mean = 0, sd = 0.1)
points(x, y, pch = 16, cex = 1.2)
x1 <- 4.25
y1 <- 4.55
points(x = x1, y = y1, pch = 8, cex = 1.2)
abline(lm(y~x), lty = 2, lwd = 1)
x1 <- c(x,x1)
y1 <- c(y,y1)
abline(lm(y1~x1), lwd = 1)
text(x = 0.2, y = 4.8, labels = "b)", cex = 1.2)
plot(x = -5, y = -5, xlim = c(0,5), ylim = c(0,5),
axes = TRUE, tcl = NA, yaxt = "n", xaxt = "n",
xlab = "", ylab = "")
abline(h = 0:5, lty = 3, col = gray(0.7))
abline(v = 0:5, lty = 3, col = gray(0.7))
x <- seq(1,2.5, length = 5)
y <- 0.5 + x + rnorm(5, mean = 0, sd = 0.1)
points(x, y, pch = 16, cex = 1.2)
x1 <- 4.50
y1 <- 1.50
points(x = x1, y = y1, pch = 8, cex = 1.2)
abline(lm(y~x), lty = 2, lwd = 1)
x1 <- c(x,x1)
y1 <- c(y,y1)
abline(lm(y1~x1), lwd = 1)
text(x = 0.2, y = 4.8, labels = "c)", cex = 1.2)
FIGURA 1: (a): Valor atípico pero sin influencia. A pesar de que su valor \(Y\) es atípico dado su valor \(X\), tiene poca influencia en la línea de regresión ya que está próxima a \(\bar{X}\). (b) Valor atípico con efecto palanca ya que tiene un alto valor de \(X\). Sin embargo, debido a que su valor de \(Y\) es próximo al pronosticado por el modelo no tiene ninguna influencia. (c) Combinación de discrepancia (valor en \(Y\) atípico) y apalancamiento (valor en \(X\) atípico) que dan como resultado una fuerte influencia. En este caso, tanto la pendiente como la intersección cambian dramáticamente.
Apalancamiento o puntos palanca (Leverage)
A veces, un punto de la recta es capaz de determinar la recta de regresión. Si consideramos la pendiente de la recta de regresión como la media ponderada de las pendientes de todas las rectas que pueden construirse pasando por el centro de los datos y cada punto de la muestra el peso de cada pendiente en esta media ponderada vendrá dado por:
\[\begin{equation} p_{i} = \dfrac{\left(x_i - \bar{x} \right)^2}{\displaystyle\sum_{j} \left(x_j - \bar{x} \right)^2} \label{equ:puntospalanca} \end{equation}\]Una conclusión de la anterior ecuación es que si existe una observación muy alejada de la media entonces
\[\begin{equation} \left( x_i - \bar{x}\right)^2 \approx \displaystyle \sum_{j} \left(x_j - \bar{x} \right)^2 \end{equation}\]y por lo tanto \(p_{i}\approx 1\), esto implica que la pendiente determinada por esta observación tendrá un peso decisivo en la estimación de la recta de regresión. Como la recta de regresión pasará por el punto \((\bar{x},\bar{y})\), si la observación tiene un alto valor de \(p_i\) se denominará puntos palanca ya que tienen la capacidad de alterar la recta de regresión.
Vamos a demostrar que \(p_i\) toma valores entre 0 y \((n-1)/n\). Si consideramos una muestra \((x_1, x_2, \ldots, x_n)\) y consideramos además que \(x_i\) es mucho mayor que las demás observaciones, su efecto palanca en regresión dado por:
\[\begin{equation} h_i = \dfrac{1}{n} + p_i = \dfrac{1}{n} + \dfrac{\left(x_i - \bar{x}\right)^2}{\displaystyle\sum_{j} \left(x_j - \bar{x} \right)^2} = \hat{n}_{i}^{-1} \label{equ:defhi} \end{equation}\]tiende a uno cuando \(x_i \rightarrow \infty\). Vamos a eliminar de \(\bar{x}\) el efecto de \(x_i\). Si denotamos por \(\bar{x}_{(i)}\) a la media de la muestra excluyendo precisamente el valor de \(x_i\), podemos poner:
\[\begin{equation} x_i - \bar{x} = x_{i} - \left( \dfrac{n-1}{n} \bar{x}_{(i)} + \dfrac{1}{n} x_i \right) = \dfrac{n-1}{n} \left( x_i - \bar{x} \right) \label{equ:relacioni} \end{equation}\]Con la relación obtenida podemos reescribir \(h_i\) de la siguiente manera:
\[\begin{equation} \begin{array}{rcl} h_i & = & \dfrac{1}{n} + \dfrac{\left(x_i - \bar{x}\right)^2}{\displaystyle\sum_{j} \left(x_j - \bar{x} \right)^2} \\ & = & \dfrac{1}{n} + \dfrac{ \left(\dfrac{n-1}{n} \right)^2 \left(x_i - \bar{x}_{(i)} \right)^2 }{ \displaystyle\sum_{j\neq i}\left(x_j - \bar{x}_{(i)} \right)^2 + \dfrac{n-1}{n}\left(x_i - \bar{x}_{(i)} \right)^2 } \end{array} \label{equ:paralimite} \end{equation}\]Si en la expresión anterior hacemos límite cuando \(x_i\rightarrow\infty\), tenemos que:
\[\begin{equation} \begin{array}{rcl} \displaystyle\lim_{x_i \rightarrow \infty} h_i & = & \dfrac{1}{n} + \displaystyle\lim_{x_i \rightarrow \infty} \dfrac{ \left(\dfrac{n-1}{n} \right)^2 \left(x_i - \bar{x}_{(i)} \right)^2 }{ \displaystyle\sum_{j\neq i}\left(x_j - \bar{x}_{(i)} \right)^2 + \dfrac{n-1}{n}\left(x_i - \bar{x}_{(i)} \right)^2 } \\ & = & \dfrac{1}{n} + \dfrac{n-1}{n} = 1 \end{array} \end{equation}\]Entonces \(p_i\) toma un valor límite de \((n-1)/n\). Dos conclusiones directas de estos resultados son:
Si \(x_i = \bar{x}\) entonces \(h_i = 1/n\), es decir, un punto situado en la media de los datos tiene el mínimo efecto palanca (\(1/n\)).
Si la distancia \(\left(x_i - \bar{x} \right)^2\) crece sin límite, el efecto palanca del punto \(x_i\) tiende a un valor máximo de 1.
A partir de la ecuación es inmediato comprobar que:
\[\begin{equation} \displaystyle\sum_{i=1}^{n} h_i = 1 + \dfrac{\displaystyle\sum_{i=1}^{n}\left( x_i - \bar{x}\right)^2}{n S_{x}^{2}} = 2 \end{equation}\]Por lo que el valor medio del efecto palanca será de \(2/n\). Una observación tiene alta influencia si (Peña 2002):
\[\begin{equation} h_i > \dfrac{6}{n} \label{equ:hinfluencia} \end{equation}\]Residuos estandarizados
Una consecuencia de que las observaciones tengan distinto peso (\(p_i\)) en la estimación del modelo es que el error en cada punto tenga distinta precisión. En cada punto se verifica la descomposición básica del modelo como puede verse en la FIGURA 2:
\[\begin{equation} y_i = \hat{y}_i + e_i \label{equ:descomposicionbasica} \end{equation}\]y al estar las variables \(\hat{y}_i\) y \(e_i\) incorreladas, tenemos que:
\[\begin{equation} Var\left(y_i | x_i\right) = \sigma^2 = Var\left( \hat{y}_i | x_i\right) + Var\left(e_i \right) \label{equ:varyi} \end{equation}\]Por otro lado, la varianza de la estimación de la media condicionada en el punto \(\hat{y}_i\) puede obtenerse a partir de las varianzas de los coeficientes de la recta de regresión. Si escribimos la recta de regresión en desviaciones a la media:
\[\begin{equation} \hat{y}_i = \bar{y} + \hat{\beta}_1\left(x_i - \bar{x} \right) \end{equation}\]Considerando que \(\bar{y}\) y \(\beta_1\) son independientes, aplicamos la varianza y sustituimos la expresión de la varianza del coeficiente de regresión:
\[\begin{equation} \begin{array}{rcl} Var\left( \hat{y}_i \right) & = & Var\left(\bar{y} \right) + \left(x_i - \bar{x}\right) Var\left(\hat{\beta}_1\right) \\ & = & \dfrac{\sigma^2}{n} + \left(x_i - \bar{x}\right)^2 \dfrac{\sigma^2}{nS_{X}^{2}} \\ & = & \sigma^2 \left( \dfrac{1}{n} + \dfrac{\left(x_i - \bar{x}\right)}{nS_{X}^{2}}\right) \\ & = & \sigma^2 h_i \end{array} \label{equ:varhatyi} \end{equation}\]Luego la varianza de la estimación de la media condicional depende del efecto palanca del punto (\(h_i\)):
Si el punto \(x_i\) está muy alejado de la media de las \(x\) (\(\bar{x}\)) y tiene efecto palanca, la variabilidad de la estimación de la media en ese punto será alta.
Si el punto \(x_i\) tiene poco efecto palanca, la variabilidad de la estimación será mucho menor.
De las anteriores ecuaciones se deduce que:
\[\begin{equation} \begin{array}{rcl} Var\left(\hat{y}_i\right) + Var\left(e_i\right) & = & \sigma^2\\ Var\left(e_i\right) & = & \sigma^2 - Var\left(\hat{y}_i\right)\\ Var\left(e_i\right) & = & \sigma^2 - \sigma^2 h_i \\ Var\left(e_i\right) & = & \sigma^2 \left( 1 - h_i\right ) \end{array} \label{equ:varei} \end{equation}\]Esta ecuación nos indica que las perturbaciones no se estiman con la misma precisión en todas las observaciones. En los puntos con alto efecto palanca (\(h_i \approx 1\)) el residuo será pequeño y por lo tanto su varianza también. Por el contrario, en los puntos con bajo efecto palanca la variabilidad del residuo será mayor. Por esta razón, se definen los residuos estandarizados, \(r_i\), de la siguiente manera:
\[\begin{equation} r_i = \dfrac{e_i}{\hat{S_{R}} \displaystyle\sqrt{1-h_i}} \label{equ:defresiduosestandarizados} \end{equation}\]Si las hipótesis del modelo son ciertas \(r_i \sim N(0,1)\). Al estar los \(r_i\) libres de unidades por la estandarización podemos valorar directamente su tamaño.
Distancia de Cook (Cook’s Distance)
Un procedimiento razonado para determinar si una observación es influyente en el modelo es estimar la ecuación de regresión con esta observación y sin ella. Si los coeficientes del modelo no varían mucho, podríamos concluir que dicha observación no es influyente. Por el contrario, si los parámetros del modelo cambian mucho concluiríamos que la observación es influyente.
Una medida del cambio en la ecuación de regresión al eliminar el punto \(i\) de la muestra puede definirse como:
\[\begin{equation} D_i = \dfrac{\left(\hat{y}_i - \hat{y}_{i(i)} \right)^2} {2 Var\left(\hat{y}_i\right)} \label{equ:defcook} \end{equation}\]Donde \(\hat{y}_i\) es el valor de la recta para \(x = x_i\), \(\hat{y}_{i(i)}\) es el valor de la recta de regresión cuando se elimina la observación \(i\) del cálculo de los parámetros de la recta y \(Var\left(\hat{y}_i\right)\) es la variabilidad del valor \(\hat{y}_i\). El valor 2 tiene en cuenta el número de parámetros estimados en el modelo. Si tenemos en cuenta que \(Var\left(\hat{y}_i \right) = \sigma^2 h_i\), obtenemos la medida de Influencia de Cook o Distancia de Cook:
\[\begin{equation} D_i = \dfrac{\left(\hat{y}_i - \hat{y}_{i(i)} \right)^2}{2\hat{S}_{R}^{2}h_i} \label{equ:defcook2} \end{equation}\]En la anterior ecuación se ha sustituido la varianza por su estimación. Se considera que una observación es influyente si \(D_i > 1\), lo que supone, teniendo en cuenta la anterior ecuación, que al eliminar dicha observación del modelo, su predicción basada en el modelo cambia en más de \(\sqrt{2}\) desviaciones típicas.

FIGURA 2: Influencia de un punto típico en las \(x\). En el caso (a) el punto \(A = (x_{A}, y_{A})\) es un punto palanca pero no tiene mucha influencia. En el caso (b) el punto \(B = (x_{B}, y_{B})\) es un punto palanca y tiene mucha influencia en el modelo.
Los puntos palanca tienen la capacidad de ser influyentes en la estimación de los parámetros de los modelos, pero la influencia real se mide mediante el estadístico de Cook. En la FIGURA 2 los puntos \((x_{A}, y_{A})\) y \((x_{B}, y_{B})\) son claramente puntos palanca, pero en el caso (a) el punto \(A\) es atípico respecto de la distribución de las \(x\) pero no respecto a \(y\) ya que, como podemos observar en la FIGURA 2, el valor \(y_{A}\) (ordenada del punto \(A\)) es próximo al valor \(\hat{y}_{A}^{(2)}\) ordenada prevista para dicho punto por la recta de ajuste sin incluir el punto \(A\). En este caso, el punto \(A = (x_{A}, y_{A})\) es un punto palanca pero no influyente. Por el contrario, el punto palanca \(B = (x_{B}, y_{B})\) es influyente, ya que la recta estimada sin el punto \(B\) predice el valor \(\hat{y}_{B}^{(2)}\) es muy distinto al predicho por la recta \(\hat{y}\) con todos los datos.
Identificar y controlar los puntos influyentes es muy importante, ya que una situación como la representada en la FIGURA 2 indican discrepancias entre alguna observación y el modelo. Las discrepancias entre observaciones influyentes y el modelo pueden ser debidas a:
El modelo es correcto y el punto \(B = (x_{B}, y_{B})\) es consecuencia de un error de medida o transcripción de dicha observación.
El valor \(B\) es correcto y el problema es que el modelo no es correcto debido a alguna de las siguientes causas:
La relación de \(x\) e \(y\) no es lineal en el intervalo \((\cdot, x_{B})\).
La relación es lineal, pero la varianza del error aumenta con \(x\), es decir, hay un problema de heterocedasticidad.
La relación es lineal y homocedástica, pero existe otra variable \(z\) que influye en \(y\) y que toma un valor distinto en el punto \(x_{B}\).
Sólo los datos no pueden ayudarnos a decidir entre las anteriores opciones, por lo que será nuestro conocimiento y experiencia del problema lo que nos ayude a discriminar entre ellas.
Existe una elevada influencia si:
\[\begin{equation} D_{i} > \dfrac{4}{n} \label{equ:distanciacookinfluencia} \end{equation}\]Donde n es el tamaño muestral. Un valor D > 1 nos indica una observación influyente.
Otras medidas de influencia
Aunque el análisis de los residuos tipificados y la distancia de Cook, son los indicadores más estudiados y utilizados, existen otras medidas para cuantificar la influencia de una observación en la estimación del modelo. A continuación describimos brevemente los DfBeta, los DfFit y el Ratio de la Covarianza.
DfBeta
Recordamos que una observación influyente es aquella que combina discrepancia con efecto palanca. Por lo tanto, otra opción razonada para valorar estas observaciones sería examinar cómo los coeficientes de regresión cambian si se omiten los valores atípicos en el modelo.
Definimos el índice \(\mbox{DfBeta}_{j(i)}\) de la siguiente manera:
\[\begin{equation} \mbox{DfBeta}_{j(i)} = \beta_j - \beta_{j(i)}\quad \forall i = 1, 2, \ldots, n\mbox{ y }j = 0, 1, \ldots, k \label{equ:defdfbeta} \end{equation}\]Donde \(\beta_j\) es el término calculado con todas las observaciones y \(\beta_{j(i)}\) está calculado sin la \(i\)-ésima observación. Este indicador mide la influencia de cada observación en los diferentes coeficientes del modelo. Se mide en términos del error estándar.
\[\begin{equation} \left| \mbox{DfBeta}_{j(i)} \right| = \left| \dfrac{\widehat{\beta}_j - \widehat{\beta}_{j(i)} }{\sqrt{\widehat{\sigma}^2_{(i)} \left(X^{T}X \right)^{-1}_{jj}}}\right| \label{equ:dfbeta} \end{equation}\]Un observación tiene influencia si tiene un efecto significativo en el coeficiente. Se dirá que una observación tiene influencia atípica si:
\[\begin{equation} \left| \mbox{DfBeta}_{j(i)}\right| > \dfrac{2}{\sqrt{n}} \label{equ:dfbetainfluencia} \end{equation}\]Donde n es el número de observaciones.
DfFit
DfFit es un indicador del leverage (apalancamiento) y altos residuos. Ésta es una medida que mide la cantidad de una observación influye en el modelo de regresión en su conjunto. La cantidad de los valores previstos cambian como resultado de inclusión y exclusión de una observación particular.
\[\begin{equation} \left| \mbox{DfFit}_{(i)} \right| = \left| {\widehat{y}_i - \widehat{y}_{i(i)} \over s_{(i)} \sqrt{h_{ii}}}\right| \label{equ:dffit} \end{equation}\]Consideramos que una observación tiene una influencia alta si:
\[\begin{equation} \left| \mbox{DfFit}_{(i)}\right| > 2\cdot \sqrt{\dfrac{k}{n}} \label{equ:dffitinfluencia} \end{equation}\]Donde k es el número de parámetros (incluido el término de intersección o independiente \(\beta_{0}\)) y n es el tamaño muestral.
Ratio de la Covarianza (Covariance Ratio)
El Ratio de la Covarianza mide el impacto de una observación en el error estándar del modelo.
\[\begin{equation} C_{i} = \frac{\left| S^2_{(i)} ({X_{(i)}'} X_{(i)})^{-1} \right|}{\left| S^2 ({X'}X)^{-1} \right| } \label{covratio} \end{equation}\]Hay un alto impacto si se cumple que:
\[\begin{equation} \left| C_{i} - 1\right| \ge 3 \cdot \dfrac{k}{n} \label{covratioinfluencia} \end{equation}\]Donde k es el número de parámetros (incluido el término de intersección o independiente \(\beta_{0}\)) y n es el tamaño muestral.
En la FIGURA 3 se muestra un ejemplo de un modelo lineal al que se le ha añadido una observación atípica (marcada en rojo) y se han analizado los diferentes indicadores de bondad del modelo y el efecto de dicha observación. En a) se muestran las observaciones y el modelo de regresión lineal. En b) se muestran las diferencias entre el valor \(y\) observado y el valor \(\hat{y}\) pronosticado por el modelo, vemos que la observación atípica destaca frente al resto por su diferencia entre \((y-\hat{y})\). En c) se analiza la distribución de los residuos estandarizados, que debieran seguir una distribución normal. En d) se analiza los residuos estandarizados comparados con el indicador de apalancamiento (leverage). En e) se muestra la distancia de Cook de cada muestra y vemos que la observación atípica tiene una distancia mucho mayor al resto de observaciones. En f) se muestra el cambio en la desviación estándar residual al eliminar cada una de las muestras y vemos que al eliminar la observación atípica la desviación estándar residual disminuye considerablemente.
En la TABLA 1 se muestra el resto de aplicar las medidas de influencia anteriormente definidas sobre los datos utilizado para representar la FIGURA 3. En la FIGURA 4 se muestran gráficamente los resultados de la TABLA 1 y observamos que no en todas las medidas la podemos deducir que nuestra observación es atípica, por ejemplo para la medida \(\mbox{DfBeta}_1\) y \(h_{ii}\). Podemos concluir entonces que nuestra observación no afecta al parámetro \(\beta_{1}\) (pendiente) pero sí afecta al parámetro \(\beta_{0}\) y que además, como es una observación central, no tiene efecto de influencia.
| x | y | \(h_i\) | \(r_i\) | Cook’s Distance | \(\mbox{DfBeta}_0\) | \(\mbox{DfBeta}_1\) | DfFit | Covariance Ratio |
|---|---|---|---|---|---|---|---|---|
| 1 | 14,440 | 0,186 | -0,914 | 0,095 | -0,434 | 0,371 | -0,434 | 1,252 |
| 2 | 16,174 | 0,159 | 0,226 | 0,005 | 0,095 | -0,079 | 0,095 | 1,325 |
| 3 | 13,519 | 0,135 | -0,237 | 0,004 | -0,090 | 0,072 | -0,091 | 1,287 |
| 4 | 11,274 | 0,114 | -0,543 | 0,019 | -0,186 | 0,142 | -0,190 | 1,224 |
| 5 | 8,583 | 0,095 | -0,999 | 0,053 | -0,309 | 0,224 | -0,324 | 1,106 |
| 6 | 10,125 | 0,080 | 0,018 | 0,000 | 0,005 | -0,003 | 0,005 | 1,219 |
| 7 | 10,799 | 0,068 | 0,722 | 0,019 | 0,167 | -0,100 | 0,193 | 1,135 |
| 8 | 6,521 | 0,059 | -0,278 | 0,002 | -0,054 | 0,027 | -0,068 | 1,182 |
| 9 | 5,680 | 0,053 | -0,097 | 0,000 | -0,015 | 0,006 | -0,022 | 1,183 |
| 10 | 15,000 | 0,050 | 3,548 | 0,334 | 0,804 | -0,125 | 1,448 | 0,107 |
| 11 | 4,471 | 0,050 | 0,425 | 0,005 | 0,039 | 0,008 | 0,096 | 1,157 |
| 12 | -1,611 | 0,053 | -1,183 | 0,039 | -0,070 | -0,072 | -0,284 | 1,007 |
| 13 | 0,949 | 0,059 | 0,159 | 0,001 | 0,004 | 0,015 | 0,039 | 1,189 |
| 14 | -0,653 | 0,068 | 0,080 | 0,000 | -0,001 | 0,011 | 0,021 | 1,203 |
| 15 | -0,565 | 0,080 | 0,586 | 0,015 | -0,027 | 0,105 | 0,170 | 1,173 |
| 16 | -2,268 | 0,095 | 0,474 | 0,012 | -0,039 | 0,104 | 0,151 | 1,209 |
| 17 | -6,674 | 0,114 | -0,592 | 0,022 | 0,070 | -0,156 | -0,208 | 1,216 |
| 18 | -6,609 | 0,135 | -0,087 | 0,001 | 0,013 | -0,027 | -0,033 | 1,294 |
| 19 | -8,784 | 0,159 | -0,380 | 0,014 | 0,073 | -0,133 | -0,161 | 1,311 |
| 20 | -12,205 | 0,186 | -1,142 | 0,149 | 0,275 | -0,470 | -0,550 | 1,185 |
set.seed(134)
x <- 1:20
y <- 17 - 1.3*x + rnorm(length(x), mean = 0, sd = 1.5)
y[10] <- 15
modelo.lm <- lm(y~x)
colores <- rep(gray(0.4), 20)
colores[10] <- colours()[556]
# MODELO ------------------------------------------------------------------
# par(mar = c(5.1, 4.1, 1.1, 1.1), mfrow = c(3, 2))
par(mfrow = c(3, 2), mar = c(5.6, 6.1, 2.1, 1.1), mgp = c(3.0, 0.8, 0))
plot(x, y, yaxt = "n",
xlim = extendrange(range(x), f = 0.08),
pch = 16, col = colores, cex = 1.8,
cex.main = 1.3, cex.lab = 1.3, cex.axis = 1.3)
abline(v = pretty(x), lty = 10, col = gray(0.7))
abline(h = pretty(y), lty = 10, col = gray(0.7))
axis(2, las = 2, cex.axis = 1.3)
abline(modelo.lm, lty = 1, lwd = 2, col = gray(0.6))
mtext(text = "a)", side = 3, line = 1, adj = -0.4)
# Y.HAT -------------------------------------------------------------------
y.hat <- predict(modelo.lm)
plot(x = y.hat,
y = y - y.hat,
ylim = extendrange(range(y - y.hat,
na.rm = TRUE),
f = 0.08),
xlab = "Fitted values",
main = "Residuals vs Fitted",
cex.main = 1.3, cex.lab = 1.3, cex.axis = 1.3,
ylab = expression(Residuals~~(y-hat(y))),
pch = 16, cex = 1.8, col = colores,
yaxt = "n"
)
axis(2, las = 2, cex.axis = 1.3)
abline(h = 0, lty = 3, col = "gray", lwd = 3)
mtext(text = "b)", side = 3, line = 1, adj = -0.4)
# NORMAL Q-Q --------------------------------------------------------------
rs <- rstandard(modelo.lm)
qqnorm(rs, main = "Normal Q-Q", cex.main = 1.2,
pch = 16, cex = 1.8, yaxt = "n",
cex.main = 1.3, cex.lab = 1.3, cex.axis = 1.3,
ylim = extendrange(range(rs, na.rm = TRUE), f = 0.08),
col = colores,
xlab = "Theoretical Quantiles",
ylab = "Standardized\nresiduals")
axis(2, las = 2, cex.axis = 1.3)
qqline(rs, lty = 3, col = gray(0.5), lwd = 2)
mtext(text = "c)", side = 3, line = 1, adj = -0.4)
# RESIDUALS VS LEVERAGE ---------------------------------------------------
plot(rstandard(modelo.lm) ~ hatvalues(modelo.lm),
main = "Residual vs Leverage",
pch = 16, cex = 1.8,
col = colores,
cex.main = 1.3, cex.lab = 1.3, cex.axis = 1.3,
xlim = range(c(0, hatvalues(modelo.lm))),
yaxt = "n",
xlab = "Leverage", ylab = "Standardized\nresiduals")
axis(2, las = 2, cex.axis = 1.3)
hh <- seq(0, 1.0, by = 0.02)
p <- 2 # Número de parámetros del modelo lineal
for (i in 1:4) {
crit <- c(0.25, 0.50, 0.75, 1.00)[i]
cl.h <- sqrt(crit * p * (1 - hh)/hh)
lines(hh, cl.h, lty = 3, col = rainbow(6)[i], lwd = 3)
lines(hh, -cl.h, lty = 3, col = rainbow(6)[i], lwd = 3)
}
abline(h = 0, lty = 2, col = gray(0.5))
abline(v = 0, lty = 2, col = gray(0.5))
legend(x = "topleft", bty = "n",
cex = 1.2,
pch = 16, col = rainbow(6)[1:4],
legend = c(0.25, 0.50, 0.75, 1.00))
mtext(text = "d)", side = 3, line = 1, adj = -0.4)
# COOK'S DISTANCE VS LEVERAGE ---------------------------------------------
cook <- cooks.distance(modelo.lm)
plot(cook, type = "h", lwd = 5,
ylim = range(c(0, cook)),
pch = 16, cex = 1.8,
col = colores,
cex.main = 1.3, cex.lab = 1.3, cex.axis = 1.3,
main = "Cook's Distance",
ylab = "Cook's Distance",
xlab = "Obs. number",
yaxt = "n")
axis(2, las = 2, cex.axis = 1.3)
mtext(text = "e)", side = 3, line = 1, adj = -0.4)
# RESIDUAL STANDARD DEVIATION ---------------------------------------------
plot(influence(modelo.lm)$sigma, type = "h", lwd = 5,
ylim = range(c(0, influence(modelo.lm)$sigma)),
col = colores, pch = 16, cex = 1.8,
cex.main = 1.3, cex.lab = 1.3, cex.axis = 1.3,
main = "Residual standard deviation",
ylab = "Residual\nstandard deviation",
xlab = "Obs. number",
yaxt = "n")
axis(2, las = 2, cex.axis = 1.3)
abline(h = summary(modelo.lm)[[6]], col = "red", lty = 1, lwd = 2)
mtext(text = "f)", side = 3, line = 1, adj = -0.4)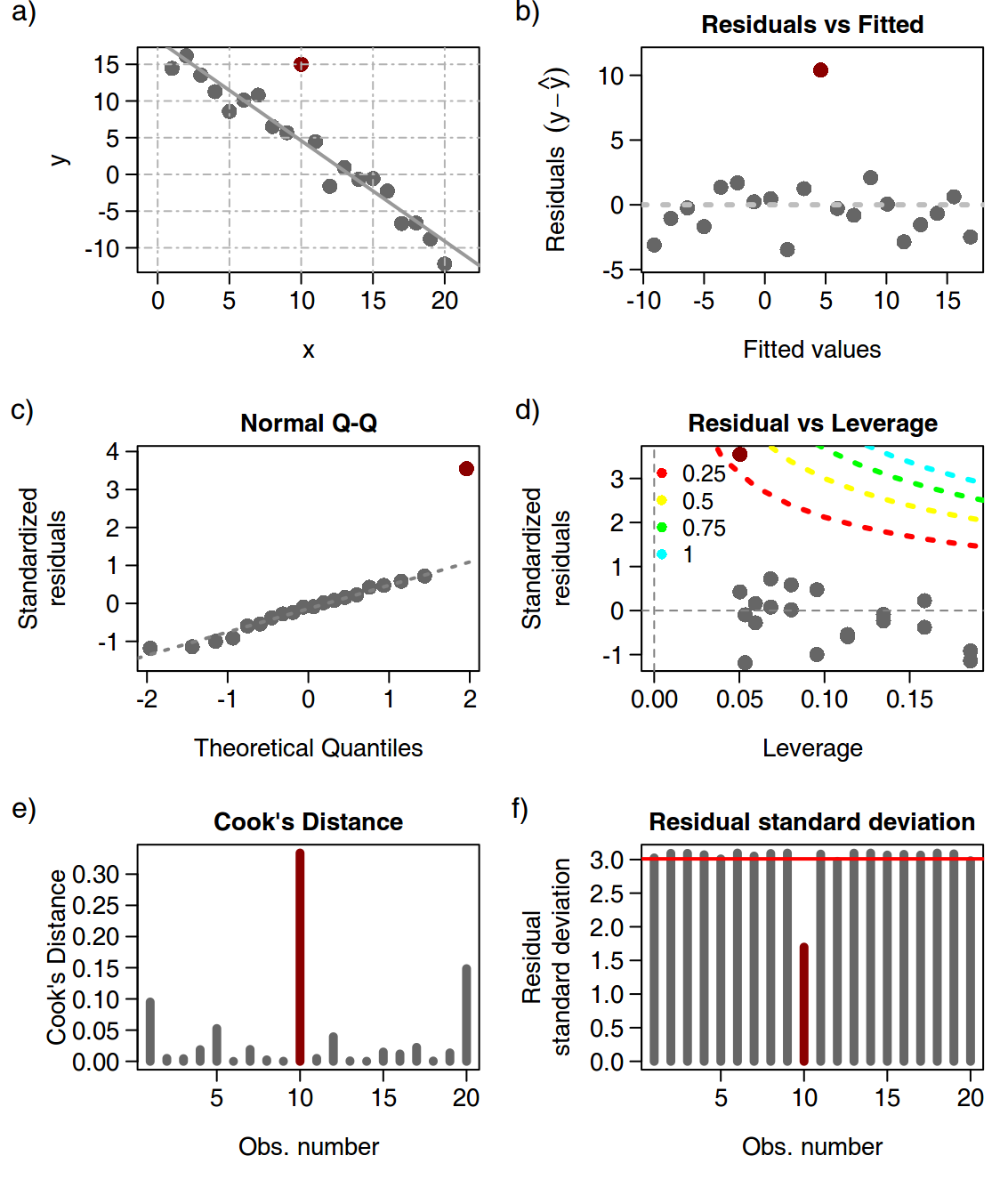
FIGURA 3: En a) se muestran las observaciones y el modelo de regresión lineal. En b) se muestran las diferencias entre el valor \(y\) observado y el valor \(\hat{y}\) pronosticado por el modelo. En c) se analiza la distribución de los residuos estandarizados. En d) se analiza los residuos estandarizados comparados con el indicador de apalancamiento (leverage). En e) se muestra la distancia de Cook de cada muestra y en f) se muestra el cambio en la desviación estandar residual al eliminar cada una de las muestras.
set.seed(134)
x <- 1:20
y <- 17 - 1.3*x + rnorm(length(x), mean = 0, sd = 1.5)
y[10] <- 15
modelo.lm <- lm(y~x)
X <- cbind(1:20,y, influence.measures(modelo.lm)$infmat)
colores <- rep(gray(0.4), 20)
colores[10] <- colours()[556]
par(mfrow = c(3,2), mar = c(2.8, 4.1, 1.1, 1.1), mgp = c(2.0,0.5, 0.0))
plot(X[, 3], type = "h",
col = colores, yaxt = "n",
ylim = extendrange(range(X[, 3]), f = 0.08),
lwd = 4,
xlab = "Observación", ylab = expression(DfBeta[0]))
axis(2, las = 2)
abline(h = 2/sqrt(20), lty = 2, col = gray(0.7))
abline(h = -2/sqrt(20), lty = 2, col = gray(0.7))
mtext("a)", side = 3, adj = -0.2, line = 0.1, cex = 0.8)
plot(X[, 4], type = "h",
col = colores, yaxt = "n",
ylim = extendrange(range(X[, 4]), f = 0.08),
lwd = 4,
xlab = "Observación", ylab = expression(DfBeta[1]))
axis(2, las = 2)
abline(h = 2/sqrt(20), lty = 2, col = gray(0.7))
abline(h = -2/sqrt(20), lty = 2, col = gray(0.7))
mtext("b)", side = 3, adj = -0.2, line = 0.1, cex = 0.8)
plot(X[, 5], type = "h",
col = colores, yaxt = "n",
ylim = extendrange(range(X[, 5]), f = 0.08),
lwd = 4,
xlab = "Observación", ylab = "DfFit")
axis(2, las = 2)
abline(h = 2*sqrt(2/20), lty = 2, col = gray(0.7))
abline(h = -2*sqrt(2/20), lty = 2, col = gray(0.7))
mtext("c)", side = 3, adj = -0.2, line = 0.1, cex = 0.8)
plot(X[, 6], type = "h",
col = colores, yaxt = "n",
ylim = extendrange(range(X[, 6]), f = 0.05),
lwd = 4,
xlab = "Observación", ylab = "Covariance Ratio")
axis(2, las = 2)
abline(h = 3*(2/20) + 1, lty = 2, col = gray(0.7))
abline(h = -3*(2/20) + 1, lty = 2, col = gray(0.7))
mtext("d)", side = 3, adj = -0.2, line = 0.1, cex = 0.8)
plot(X[, 7], type = "h",
col = colores, yaxt = "n",
ylim = extendrange(range(X[, 7]), f = 0.05),
lwd = 4,
xlab = "Observación", ylab = "Cook's Distance")
axis(2, las = 2)
abline(h = 4/20, lty = 2, col = gray(0.7))
mtext("e)", side = 3, adj = -0.2, line = 0.1, cex = 0.8)
plot(X[, 8], type = "h",
col = colores, yaxt = "n",
ylim = extendrange(range(c(0,X[, 8])), f = 0.05),
lwd = 4,
xlab = "Observación", ylab = expression(h[ii]))
axis(2, las = 2)
abline(h = 2*2/20, lty = 2, col = gray(0.7))
mtext("f)", side = 3, adj = -0.2, line = 0.1, cex = 0.8)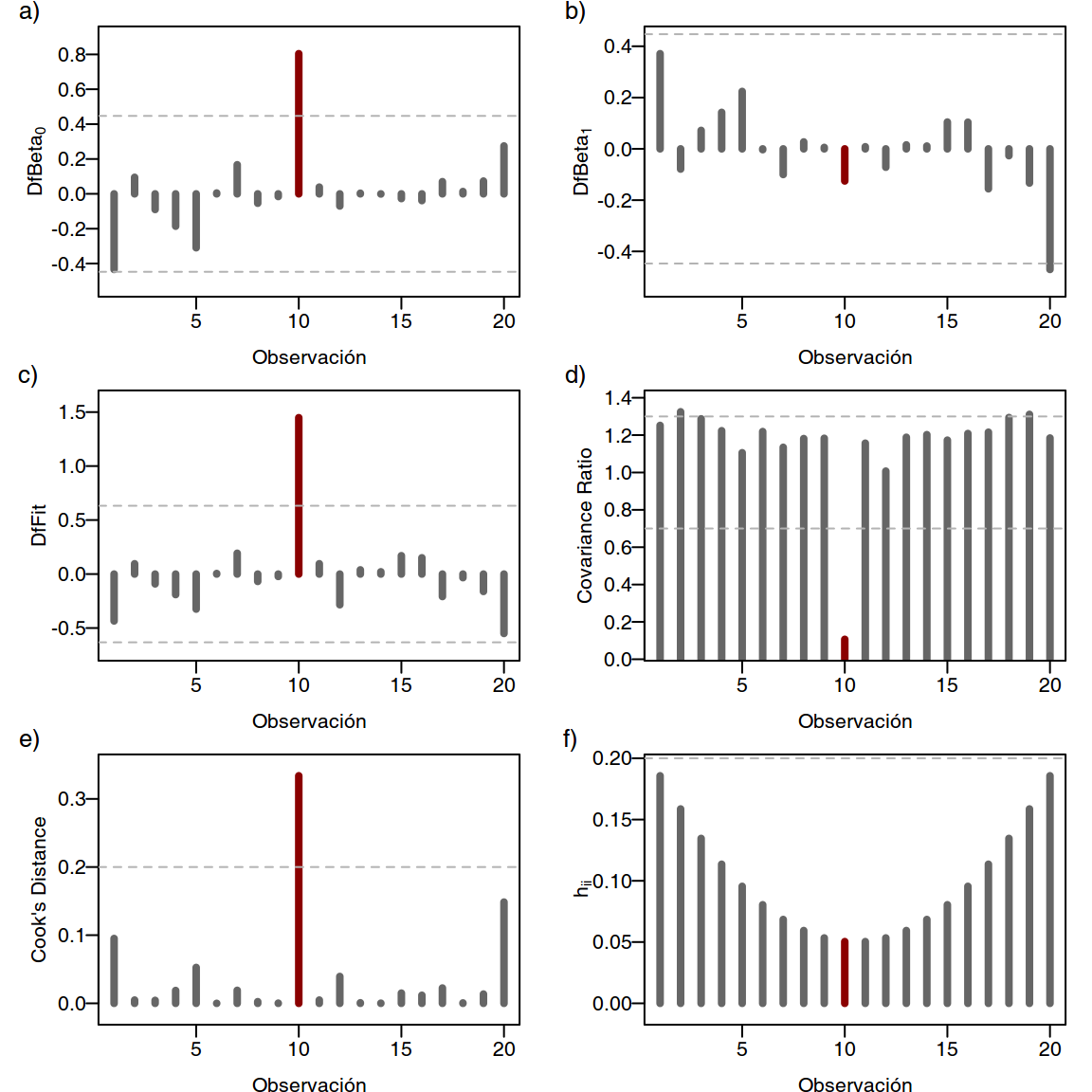
FIGURA 4: En a) se muestran los valores de \(\mbox{DfBeta}_0\), en b) se muestran los valores de \(\mbox{DfBeta}_1\), en c) se muestran los valores individuales de dffit, en d) se muestra el valor de Covariance Ratio, en e) se muestra la Distancia de Cook y en f) los valores \(h_{ii}\) de cada observación. Se ha coloreado la muestra atípica y observamos que no en todos los indicadores nuestra observación es atípica, por ejemplo para los indicadores \(\mbox{DfBeta}_1\) y \(h_{ii}\).
Bibliografía
Altman, Naomi, and Martin Krzywinski. 2015. “Simple Linear Regression.” Nature Methods 12 (11): 999–1000.
———. 2016a. “Points of Significance: Analyzing Outliers: Influential or Nuisance?” Nature Methods 13 (4): 281–82.
———. 2016b. “Points of Significance: Regression Diagnostics.” Nature Methods 13 (5): 385–86.
Armitage, Emily G., and Coral Barbas. 2014. “Metabolomics in Cancer Biomarker Discovery: Current Trends and Future Perspectives.” J Pharm Biomed Anal 87 (January). Centre for Metabolomics; Bioanalysis (CEMBIO), Faculty of Pharmacy, Universidad San Pablo CEU, Campus Monteprincipe, Boadilla del Monte, 28668 Madrid, Spain.: 1–11. doi:10.1016/j.jpba.2013.08.041.
Cook, R.D., and S. Weisberg. 1982. Residuals and Influence in Regression. Monographs on Statistics and Applied Probability. Chapman & Hall.
Čuperlović-Culf, Miroslava. 2013. “5 - Metabolomics Data Analysis – Processing and Analysis of a Dataset.” In {NMR} Metabolomics in Cancer Research, edited by Miroslava Čuperlović-Culf, 261–333. Woodhead Publishing Series in Biomedicine. Woodhead Publishing. doi:http://dx.doi.org/10.1533/9781908818263.261.
Fox, J. 1997. Applied Regression Analysis, Linear Models, and Related Methods. SAGE Publications.
Krzywinski, Martin, and Naomi Altman. 2014. “Points of Significance: Two-Factor Designs.” Nature Methods 11 (12): 1187–8.
Kuehl, R.O., and M.G. Osuna. 2001. Diseño de Experimentos: Principios Estadísticos de Diseño Y análisis de Investigación. Matemáticas (Thomson). International Thomson Editores, S. A. de C. V.
Martínez-Arranz, Ibon, Rebeca Mayo, Miriam Pérez-Cormenzana, Itziar Mincholé, Lorena Salazar, Cristina Alonso, and José M. Mato. 2015. “Enhancing Metabolomics Research Through Data Mining.” Journal of Proteomics 127, Part B (0): 275–88. doi:http://dx.doi.org/10.1016/j.jprot.2015.01.019.
Peña, D. 2002. Regresión Y Diseño de Experimentos. El Libro Universitario. Manuales. Alianza.
Pulido, H.G., R. de la Vara Salazar, P.G. González, C.T. Martínez, and M.C.T. Pérez. 2004. Análisis Y Diseño de Experimentos. McGraw-Hill.
Weiner, I.B., D.K. Freedheim, J.A. Schinka, and W.F. Velicer. 2003. Handbook of Psychology, Research Methods in Psychology. Handbook of Psychology. Wiley.
Xie, Yihui. 2014. “Knitr: A Comprehensive Tool for Reproducible Research in R.” In Implementing Reproducible Computational Research, edited by Victoria Stodden, Friedrich Leisch, and Roger D. Peng. Chapman; Hall/CRC. http://www.crcpress.com/product/isbn/9781466561595.
———. 2015. Dynamic Documents with R and Knitr. 2nd ed. Boca Raton, Florida: Chapman; Hall/CRC. http://yihui.name/knitr/.
———. 2016. Knitr: A General-Purpose Package for Dynamic Report Generation in R. http://yihui.name/knitr/.